Anisotropic Materials

Light propagation

So war we have only discussed isotropic materials, meaning that the speed of light was independent by the direction of light propagation in the material. Often, the light propagation is, however, not isotropic as the underlying materials have an anisotropic structure.

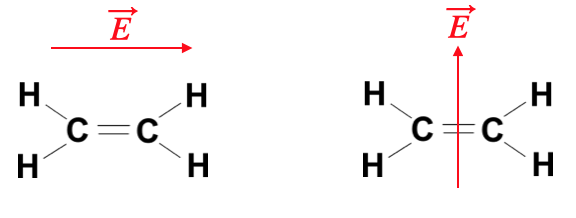
Figure 1— Ethene molecules as an example for an anisotropically polarizable object. The red arrows denote the electric field directions.

Just consider the above molecule $C_{2} H_{4}$ (Ethen), where the two carbon atoms are bound by a double bond. In an external electric field aligned along that bond, we certainly expect the electrons to be more easily displaced over a larger distance, when the field is aligned parallel to the double bond. The dipole induced will therefore depend on the orientation of molecule and electric field. We therefore need to express the electronic polarizability $α$ for the calculation of the dipole moment $\vec{p} = α \vec{E}$ as a tensor $\overset{\leftrightarrow}{a}$ .

$\overset{\leftrightarrow}{a} = (\begin{matrix} α_{11} & α_{12} & α_{13} \\ α_{21} & α_{22} & α_{23} \\ α_{31} & α_{32} & α_{33} \end{matrix})$

Consequently also the susceptibility $χ$ , the dielectric function $ϵ_{r}$ and refractive index $n$ will be tensors in anisotropic materials. The entries of these tensors now depend on the choice of the coordinate system, since the polarisabilities are connected to the structures. Accordingly, there is also coordinate system in which the tensor becomes completely diagonal.

$\begin{matrix} (dielectric tensor) & \overset{\leftrightarrow}{ϵ_{r}} = (\begin{matrix} ϵ_{11} & 0 & 0 \\ 0 & ϵ_{22} & 0 \\ 0 & 0 & ϵ_{33} \end{matrix}) \end{matrix}$

This coordinate systems is the principle coordinate system of the tensor. The electric displacement field $\vec{D}$ is related to the electric field $\vec{E}$ by

$\vec{D} = ϵ_{0} \overset{\leftrightarrow}{ϵ_{r}} \vec{E}$

and in the principle coordinate system of the tensor we obtain

$(\begin{matrix} D_{1} \\ D_{2} \\ D_{3} \end{matrix}) = (\begin{matrix} ϵ_{0} ϵ_{11} E_{1} \\ ϵ_{0} ϵ_{22} E_{2} \\ ϵ_{0} ϵ_{33} E_{3} \end{matrix})$

From this it becomes evident, that the displacement field $\vec{D}$ is not anymore parallel to the electric field $\vec{E}$ . The dielectric tensor and refractive index tensor are directly related through $n_{i j} = \sqrt{ϵ_{i j}}$ . In the principal coordinate system, where both tensors are diagonal, the principal refractive indices are simply the square roots of the principal dielectric constants. This relationship allows us to visualize the optical properties through the index ellipsoid. This also means now, that the wavevector $\vec{k}$ is now perpendicular to the displacement field and not to the electric field. The magnetic field is still directed along the same direction and thus the Poynting vector is not parallel to the wavevector. Energy and phasefronts flow in different directions.The sketch below indicates the relations of the vectors.

Energy Flow in Anisotropic Materials

In anisotropic materials, the direction of energy flow (given by the Poynting vector $\vec{S} = \vec{E} \times \vec{H}$ ) generally differs from the direction of phase propagation (given by the wavevector $\vec{k}$ ). This is because $\vec{E}$ and $\vec{D}$ are not parallel in anisotropic media. While the wavevector $\vec{k}$ determines the direction of phase velocity and is perpendicular to the wavefronts, the energy actually flows in the direction of the Poynting vector $\vec{S}$ . This direction is always perpendicular to the k-surface at the point where $\vec{k}$ intersects it. This explains why a single incident beam can split into two beams (ordinary and extraordinary) traveling in different directions through the material, even though their wavefronts remain parallel.

Figure 2— Sketch of the relations between the electric field $\vec{E}$ , the displacement field $\vec{D}$ , the wavevector $\vec{k}$ and the magnetic field $\vec{H}$ .

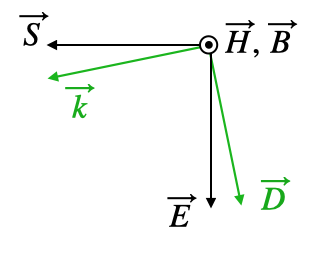
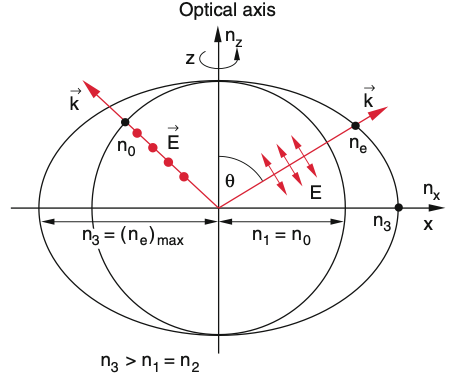
The tensorial nature of the dielectric function has now consequences for the propagation of light. In general different symmetries are considered. If we have for example two of the diagonal elements be equal to each other

$ϵ_{11} = ϵ_{22} \neq ϵ_{33}$

then we call the material uniaxial. The system has one optical axis. In case

$ϵ_{11} \neq ϵ_{22} \neq ϵ_{33} \neq ϵ_{11}$

we call the material biaxial and the material has two optical axes. We will have a look at the meaning of an optical axis a bit later.

A tensor as the dielectric tensor (similar to the tensor of inertia) can be geometrically represented by an ellipsoid with three different half axes as depicted below. This can be done for the refractive index or the dielectric tensor. When doing so with the refractive index, we obtain an index ellipsoid, where the half-axes correspond to the three refractive indices $n_{1} = \sqrt{ϵ_{11}}$ , $n_{2} = \sqrt{ϵ_{22}}$ and $n_{3} = \sqrt{ϵ_{33}}$ .

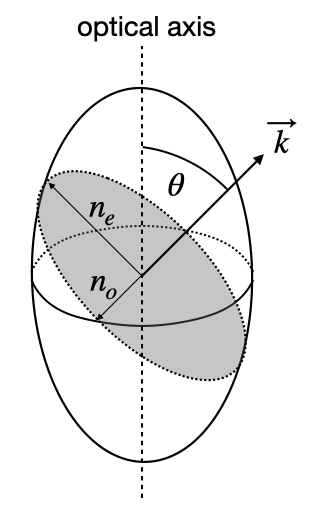
Figure 3— Index ellipsoid for a uniaxial material and a construction of the refractive indices. The k-vector cuts the ellipsoid in one point. The plane perpendicular to the k-vector intersects the ellipsoid in an ellipse. The long and short axis of the ellipse correspond to the normal modes of the material.

To find out the relevant refractive indices for a certain propagation direction on now undertakes the following steps:

chose a direction of light propagation with the direction of the wavevector $\vec{k}$
construct a plane perpendicular to the wavevector
take the intersection of this plane with the ellisoid, which is in general an ellipse
the ellipse has a long and a short axis, which correspond to the direction of the so-called normal modes
a $\vec{D}$ field along those half-axes propages with the corresponding refractive index $n_{o}$ (ordinary), $n_{e}$ (extra_ordinary)

Normal Modes in Anisotropic Materials

Normal modes are specific directions of the displacement field $\vec{D}$ for which the light wave can propagate through the anisotropic medium without changing its polarization state. These modes correspond to the major and minor axes of the ellipse formed by intersecting the index ellipsoid with a plane perpendicular to the propagation direction. For a given propagation direction, there are always two orthogonal normal modes, each associated with a specific refractive index (ordinary or extraordinary). Any other polarization state can be expressed as a superposition of these two normal modes, but will generally change as the wave propagates through the medium due to the different phase velocities of the two modes.

An optical axis is now a propagation direction, for which the refractive index does not depend on the direction of the electric field. For a biaxial material, there are two distinct directions for a propagation, while there is only one for uniaxial.

Considering now in more detail the propagation of light as a function of the direction of light propagation one obtains a dispersion relation (how the wavenumber depends on teh direction for a given frequency of light). This surface is the so-called k-surface, which in general consists of 2 sheets. This k-surface is obtained from Maxwells equations

$\begin{aligned} \vec{k} \times \vec{H} & = - ω \vec{D} \\ \vec{k} \times \vec{E} & = ω μ_{0} \vec{H} \end{aligned}$

which leads to

$\vec{k} \times (\vec{k} \times \vec{E}) + ω^{2} μ_{0} ϵ_{0} \overset{\leftrightarrow}{ϵ_{r}} \vec{E} = 0$

This equation leads to a system of equations for the components of the wavevector ( $\vec{k} = {k_{1}, k_{2}, k_{3}}$ ) that define the k-surface for a given frequency.

The k-surface represents all possible wavevectors at a given frequency in the material. For a uniaxial crystal, this surface consists of two sheets: a sphere representing the ordinary waves and an ellipsoid representing the extraordinary waves. Where these surfaces intersect defines the optical axis, along which the ordinary and extraordinary waves travel with the same phase velocity. This geometric representation helps visualize how light propagates in different directions through the crystal.

Figure 4— K-surface for a uniaxial material. The circular surface corresponds to the ordinary refractive index and the elliptical surface to the extra-ordinary refractive index. The polarization of the electric field is indicated.

If we select now a specific direction of propagation for the light with the direction of $\vec{k}$ , the intersections of the k-surface with the k-vector deliver the solutions for the refractive indices. From the figure above, it becomes obvious, that the electric field vector must be perpendicular to the plane in the case of the ordinary refractive index. Only in this case, the wavevector can be rotated in the above sketch such that the direction of the electric field does not change. If the electric field is within the plane of the above sketch, the field direction with respect to the crystal structure changes and therefore the refractive index changes.

The ordinary ray corresponds to light where the electric field is perpendicular to the plane containing the optical axis and the direction of propagation, while the extraordinary ray corresponds to light where the electric field has a component parallel to this plane. The association with s- or p-polarization depends on the orientation of the crystal’s optical axis relative to the plane of incidence.

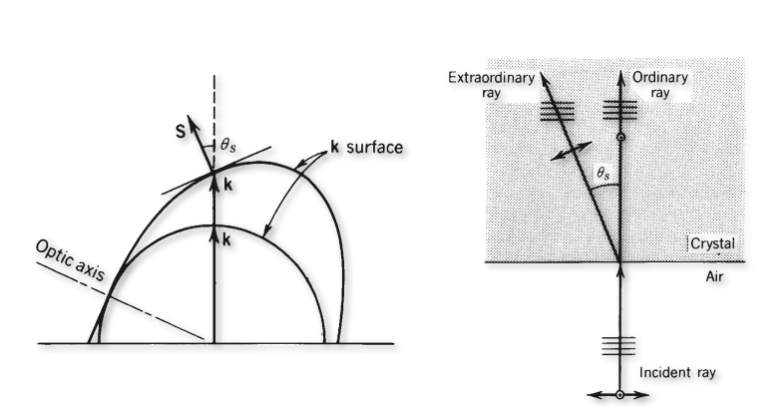
Let’s discuss the sketches above, which show the general case of birefringence. The image on the left side shows an interface between air on the bottom and the anisotropic material on the top. The wavevector is incident from below and is normal zo the surface. Its direction will intersect both k-surfaces and thereby select the ordinary refractive index and the extra-ordinary refractive index for the two different polarization directions. Both waves propgate in the same direction, so their wavefronts are perpendicular to the k-vectors as shown in the middle sketch. Yet, the Poynting vectors go in different direction. The Poynting vector, which points in the direction of energy propagation, is always perpendicular to the k-surface, since the k-surface is an isoenergy surface (think about that for a moment). This means that the beam is split into two beams with parallel wavefronts as indicated. This phenomenon is called birefringence and separates two orthogonal polarizations into two beams as indicated.

This effect is probably best visible, when you put a birefringent material like the common calcit crystal on a newpaper or book. You will immediately see the birefringence in the double images as in the figure above to the right.

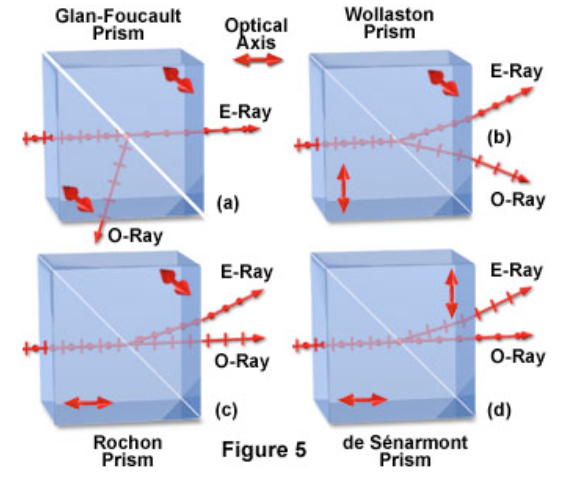
The different refractive index for both polarizations make those materials very suitable for the creating polarizing optical elements like beam splitters. A selection of different polarizing beam splitters is shown in the image below.

Figure 6— Polarizing beam splitters. Glan-Foucault prism, Wollaston prism, Rochon prism and de Senarmont prism. All of them are based on birefringence and consist of two prisms with different refractive indices for the two polarizations.

Birefringence is often observed in mechanically stressed materials like quickly cooled glasses or stretched polymer foils. The latter is demonstrated in the images below, where we used

Figure 7— Scotch tape art. Scotch tape christmas tree and tulip between crossed polarizers showing their birefringent behavior.

Wave retarders

Wave retarders are essential optical components that manipulate the polarization state of light by exploiting the different phase velocities of ordinary and extraordinary waves in anisotropic materials. These components are fundamental in many optical systems, from liquid crystal displays to laser systems and optical communications. Anisotropic materials can now but cut in specific way, for example such that the optical axis is parallel to the interface as in the picture below. Under these circumstances at normal incidence both wavevectors and both Poynting vectors of the polarizations propagate along the same direction. Yet, the p-polarization has a lower phase velocity (long k-vector) than the s-polarization. If now the incident light has now elecric field components parallel and perpedicular to the optical axis which are of same amplitude, then one component of the incident polarization is delayed in its phase with respect to the other comonent.

Let

$\vec{E} = (E_{0 x} {\hat{e}}_{x} + E_{0 y} {\hat{e}}_{y}) e^{i (ω t - k z)}$

be the incident electric field of the plane wave travelling along the z-direction with $E_{0 x} = E_{0 y}$ and the optical axis aligned along the y-axis. Then each vector component of the wave travels with a different wavevector

$\begin{aligned} E_{x} & = E_{0 x} e^{i (ω t - n_{e} k_{0} z)} \\ E_{y} & = E_{0 y} e^{i (ω t - n_{o} k_{0} z)} \end{aligned}$

After a material of thickness $d$ both components have accumulated a phase shift of

$Δ ϕ = (n_{e} - n_{o}) k_{0} d$

Quarter Wave Plate

Figure 8— Sketch of the conditions for a wave retarder. Both ordinary and extra-ordinary wave propagate in the same direction, but with different phase velocities. The phase difference between the two components is $Δ ϕ$ . The right side shows the resulting circular polarization.

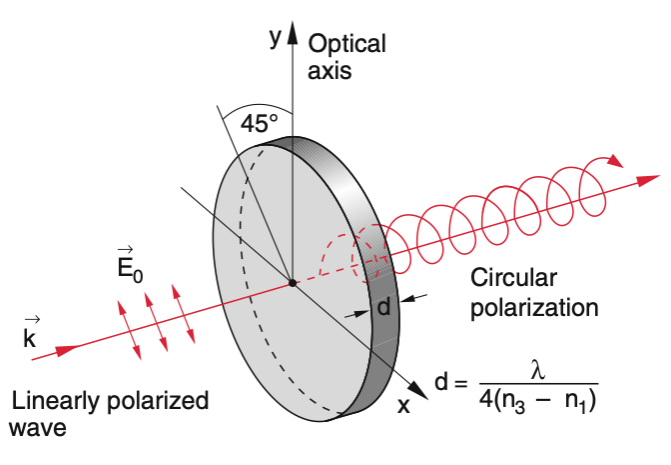
If we design now a material of a certain thickness such that the phase shift is $Δ ϕ = π / 2$ , then the light exiting the material will be circularly polarized as in the sketch on the right side. The minimum thickness of the crystal is then

$d = \frac{π}{2} \frac{1}{k_{0} (n_{e} - n_{o})} = \frac{λ}{4 (n_{e} - n_{o})}$

The crystal thickness is, however, not restricted to this minimal thickness, but to any thickness which creates a phase difference of $π / 2$ . Such an optical element which is generating a phase difference of $π / 2$ between the different electric field components with respect to the optical axis is called a Quarter Wave Plate, since the phase difference corresponds to a quarter wavelength.

If the two elecric field components are not of equal amplitude, then a quarter wave plate will generate elliptically polarized light. Note that if you send circular polarization to a QWP, linearly polarized light will be created.

Half Wave Plate

A half wave plate creates a phase difference of $π$ (half a wavelength) between the two electric field components. When linearly polarized light passes through a half wave plate, its polarization direction is rotated. The component of the electric field parallel to the optical axis experiences the extraordinary refractive index $n_{e}$ , while the perpendicular component experiences the ordinary refractive index $n_{o}$ . The $π$ phase shift effectively flips the sign of the component perpendicular to the optical axis.

When linearly polarized light is incident at an angle $θ$ with respect to the optical axis, the output polarization will be rotated to an angle $2 θ$ with respect to the optical axis but on the opposite side. This means the total rotation of the polarization direction is $2 θ$ . For example, if the incident polarization makes a $30 °$ angle with the optical axis, the output polarization will be rotated by $60 °$ with respect to the original direction. The special case of $45 °$ input leads to a $90 °$ rotation of the polarization.

The minimum thickness of a half wave plate is given by:

$d = \frac{π}{k_{0} (n_{e} - n_{o})} = \frac{λ}{2 (n_{e} - n_{o})}$

Similar to the quarter wave plate, any thickness which creates a phase difference of $π$ can be used as a half wave plate. The actual thickness used in practice is often chosen based on manufacturing constraints and the specific wavelength range for which the plate is designed.